Два этапа: детекция и декодирование

В статье две ключевые части:

1) Детекция тэга (попытка найти темные четырехугольники - это внешние границы)

2) Система декодирования обнаруженного тэга (в тэге можно хранить числа чтобы различать один тэг от другого)

В прошлой статье обсуждается первый этап детекции.

Сегодня же мы обсудим только второй этап - детекции, т.е. обнаружения тэгов.

Итак предполагается что мы нашли много черных четырехугольников - предполагаемых тэгов. Теперь надо для каждого из них решить две задачи:

• Правда ли что это тэг?

• Декодировать уникальный идентификатор этого тэга

Вытаскиваем внутреннюю часть тэга

We compute the 3×3 homography matrix that projects 2D
points in homogeneous coordinates from the tag’s coordinate
system ... to the 2D image coordinate system.

Итак раз мы знаем у тэга границы, то мы знаем его углы, находим матрицу гомографии \(H\) как делали это раньше (при сопоставлении SIFT-ключевых точек).

Но теперь у нас всего четыре “ключевые” точки - это углы тэга на картинке которые хотят перейти в новую систему координат - в углы идеального квадрата:

Теперь мы работаем с правой картинкой. Обратите внимание что там может быть не тэг а полная ерунда в случае если это ложно-положительное срабатывание.

Давайте бинаризируем наш тэг - теперь все яркие пиксели белые, а все темные пиксели - черные. Затем рассечем наш квадрат на 8 линий и 8 столбцов.

В каждой образовавшейся клетке либо \(0\) либо \(1\) - в зависимости от того каких пикселей больше - черных или белых.

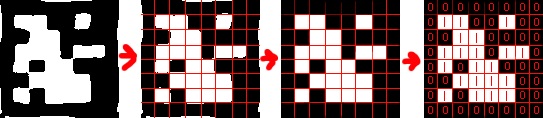
Заметьте что крайние ячейки всегда должны быть заполнены нулями (это черный край помогающий нашему первому этапу - обнаружению тега).

Мы можем например считать что это не тег, если хотя бы одна из крайних ячеек не засчиталась как \(0\) (хотя должна быть равна \(0\) в случае корректного тэга).

Кодировка

Пусть у нас есть 6x6 бит (из внутренних клеток). Выпишем их в ряд - получим 36 битное число.

Теперь речь пойдет не про обработку картинок, а про то как кодировать информацию с учетом того что информация могла быть передана с ошибками (ошибками декодирования или шумом в фотографии или это может быть вызвано несовершенством алгоритма).

Более того - мы хотим понимать в случае когда полученные биты не имеют смысла и являются шумом - т.е. хотим отдать долг ложным срабатываниям обнаружения тега - и поняв что это на самом деле не тег а ошибка - проигнорировать его.

Как же тогда кодировать числа?

Lexicode - устойчивость к ошибкам

We propose the use of a modified lexicode [24]. Classical
lexicodes are parameterized by two quantities: the number
of bits n in each codeword and the minimum Hamming
distance between any two codewords d. Lexicodes can
correct ⌊(d − 1)/2⌋ bit errors and detect d/2 bit errors.
For convenience, we will denote a 36 bit encoding with a
minimum Hamming distance of 10 (for example) as a 36h10
code

Итак они предлагают из всех возможных 36 битных чисел оставить для использования только такие, что между любыми двумяи из них есть хотя бы \(d\) разных бит.

В таком случае предложенная кодировка сможет гарантировать следующие свойства:

• Результат будет корректен если у нас меньше чем \((d-1)/2\) ошибок в битах

• Ошибка в результате будет обнаружена если у нас меньше чем \(d/2\) ошибок в битах

Для удобства кодировку на 36 битах с \(d=10\) они называют 36h10 (буква h - от слова Hamming, т.к. число разных бит - это расстояние Хэмминга).

Lexicodes derive their name from the heuristic used to
generate valid codewords: candidate codewords are considered
in lexicographic order (from smallest to largest), adding
new codewords to the codebook when they are at least a
distance d from every codeword previously added to the
codebook. While very simple, this scheme is often very close
to optimal [25].

Как же найти подходящие нам 36 битные числа? Как составить словарь?

Предлагается жадным образом добавлять очередное число в словарь только если это слово не сломает правило про минимальное рассточние Хэмминга между словами (хотя бы \(d\) разных бит).

Устойчивость к повороту тэга

In the case of visual fiducials, the coding scheme must be
robust to rotation. In other words, it is critical that when
a tag is rotated by 90, 180, or 270 degrees, that it still
have a Hamming distance of d from every other code. The
standard lexicode generation algorithm does not guarantee
this property. However, the standard generation algorithm
can be trivially extended to support this: when testing a
new candidate codeword, we can simply ensure that all four
rotations have the required minimum Hamming distance.
The fact that the lexicode algorithm can be easily extended
to incorporate additional constraints is an advantage of our
approach.

Но обратите так же внимание что тэг может поворачиваться, мы хотим не путать из-за этого что за число нам показывают.

В таком случае жадное порождение словарика надо лишь слегка расширить - слово добавляется только если оно и 3 его слова-побратима (полученных поворотами на 90 градусов) тоже проходят проверку на минимальное Хэмминг расстояние со всеми остальными словами (включая их слова-побратимы).

Устойчивость к встречаемому в природе

Some codewords, despite satisfying the Hamming distance
constraint, are poor choices. For example, a code word
consisting of all zeros would result in a tag that looks like
a single black square. Such simple geometric patterns commonly
occur in natural scenes, resulting in false positives.
The ARTag encoding system, for example, explicitly forbids
two codes because they are too likely to occur by chance

Некоторые кодовые слова могут быть не специальным тэгом - а просто совпадением. Например тэг полностью из нулей - это просто черный квадрат, в таком случае например стол может быть ошибочно интерпретирован как такой ненадежный тэг.

Rather than identify problematic tags manually, we further 
modify the lexicode generation algorithm by rejecting
candidate codewords that result in simple geometric patterns.
Our metric is based on the number of rectangles required to
generate the tag’s 2D pattern.
For example, a solid pattern
requires just one rectangle, while a black-white-black stripe
would require two rectangles (one large black rectangle with
a smaller white rectangle drawn second). 

Чтобы автоматически оценить “простоту” или “сложность” рассматриваемого паттерна - они решают задачу “сколько прямоугольников нужно чтобы нарисовать такой тэг”.

Итого

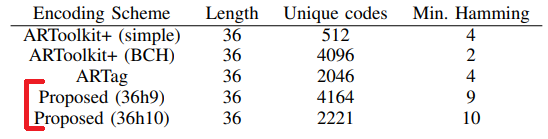
Итого мы используем подмножество 36-битных чисел такое что между любыми двумя кодами есть большая разница - много бит выглядят по-разному. Кроме того все используемые коды выглядят достаточно сложно чтобы мы крайне мало шансов имели встретить что-то в мире случайно оказавшееся похожим на корректный тэг.

Хотя генерация словаря корректных тэгов с учетом всех описанных деталей может быть вычислительно тяжелой и медленной - это не страшно, т.к. достаточно сделать это один раз и сохранить перечень получившихся кодов в файл-словарь.

Пример сколько корректных тэгов при допустимом минимальном расстоянии Хэмминга \(d=9\) и \(d=10\) между кодами в нашем словариками: