План на урок

1) Делаете задания 11-15 как и новое домашнее задание ниже (но вариант номер \(4 + (N \bmod 5)\) и как только выполните - позовите меня чтобы я отметил ваш успех и подсказал с проблемными заданиями)

2) Прорешиваете те задания которые не смогли сделать дома или в которых не были уверены (не стесняйтесь спрашивать помощи)

3) Прорешиваете те задания, которые неправильно решили на контрольной или в которых просто сомневались (но теперь оба варианта)

4) Прочитайте комментарии по заданиям вызвавшим затруднения (2, 5, 9, 10), решите хотя бы по одной задаче из них

Домашнее задание

Пусть ваш номер в списке класса \(N\).

Тогда откройте вариант номер \(3 + (N \bmod 5)\) - т.е. один из этих вариантов:

• Вариант 3

• Вариант 4

• Вариант 5

• Вариант 6

• Вариант 7

1) Выполните задания 11-15.

2) Все возникшие затруднения запишите чтобы спросить на следующем уроке.

3) Сохраните ссылку с результатами первой попытки.

4) Задания с неправильным ответом (если не все правильно) выполните еще раз неспеша и аккуратно.

5) Отправьте мне ссылку на первую попытку.

6) И будет совсем здорово если вы сможете коротко обозначить затруднения которые возникли по мере выполнения - я либо смогу вам подсказать сразу (пока ваши воспоминания свежи) либо как минимум смогу подготовиться к следующему уроку и проговорить проблемные места.

Комментарии и подсказки к некоторым заданиям 11-15 (будут пополняться)

Задание 12 (ip-адрес, маска подсети)

Как например рассказано на википедии: маска подсети позволяет понять какая часть ip-адреса указывает на адрес подсети в интернете (старшие биты помеченные единицами), а какая часть указывает на адрес узла в подсети (младшие биты помеченные нулями).

В таком случае сколько узлов может быть в рамках одной подсети? Столько сколько разных адресов узла в подсети, т.е. сколько разных комбинаций может быть в младших битах ip-адреса (те что помечены в маске подсети нулями). Т.е. \(2^n\), где \(n\) - сколько нулевых бит в маске подсети.

Обратите внимание что если говорится найти число возможных узлов в подсети если два адреса уже заняты (например адрес сети и шировещательный адрес), то нужно просто вычесть эти два адреса и получить \(2^n-2\).

Задание 14 (про замену подстрок в цикле)

Вот один из подходов к решению на примере этого задания:

-111+2
-111+2
-111+2
-222+1
-111+2

т.е. -11х1 и +1х2, т.е. за первые четыре итерации из 77х1 перешли в 1х2,66х1

-111+2
-111+2
-222+1
-111+2

т.е. -8х1, т.е. теперь мы в 1х2,58х1
дальше опять -8х1, т.е. теперь мы в 1х2,50х1
дальше 1х2,42х1
дальше 1х2,34х1
дальше 1х2,26х1
дальше 1х2,18х1
дальше 1х2,10х1
теперь аккуратно (почти до 5 единиц добрались, цикл может прерваться):

-111+2=2x2,7x1
-111+2=3x2,4x1
и на этот раз в цикл не заходим, т.к. нет пяти единиц

Обратите внимание что вариантов нотации может быть много, вам могут быть удобнее другие обозначения. Главное чтобы вы легко могли читать такую запись, тогда вам будет очень удобно, легко и надежно проверить ваше решение еще раз по этой записи.

Так же обратите внимание что сначала было 5 выполненных команд, а затем 4. И циклично повторяются эти четыре команды. Это потому что изначально у нас нет двойки в строке, но после каждой итерации цикла хотя бы одна двойка есть, и поэтому чистый цикл с самого начала выделить не вышло.

Задание 15 (поиск числа путей)

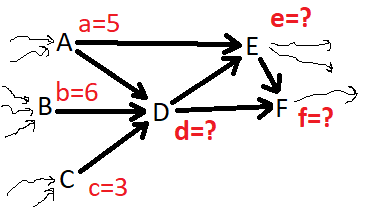
Основная идея:

1) Пусть мы уже поняли что до \(A\), \(B\), \(C\) вариантов добраться \(a=5\), \(b=6\) и \(c=3\) соответственно.

2) Тогда добраться до вершины \(D\) вариантов \(d=a+b+c\), до \(E\) - \(e=a+d\), до \(F\) - \(f=d+e\).

3) Но пока не посчитано \(d\) - не выйдет посчитать \(e\) и \(f\), поэтому мы считаем сначала для тех вершин для которых все входящие ребра уже посчитаны (точнее посчитаны вершины из которых эти ребра идут).

4) На иллюстрации в “все готово” состоянии находится только вершина \(D\), поэтому сначала считаем ее \(d=a+b+c=14\).

5) Теперь для \(E\) “все готово” - \(e=a+d=19\).

6) И наконец \(f=d+e=33\).