ЕГЭ: задания 1-10
План на урок
Разбираемый на уроке вариант - Тренировочный вариант ЕГЭ по информатике №8.
Варианты самостоятельной работы на уроке: Вариант 1, Вариант 2.
Домашнее задание
Пусть ваш номер в списке класса \(N\).
Тогда откройте вариант номер \(3 + (N \bmod 5)\) - т.е. один из этих вариантов:
1) Выполните первые десять заданий.
2) Все возникшие затруднения запишите чтобы спросить на следующем уроке.
3) Сохраните ссылку с результатами первой попытки.
4) Задания с неправильным ответом (если не все правильно) выполните еще раз неспеша и аккуратно.
5) Отправьте мне ссылку на первую попытку.
6) И будет совсем здорово если вы сможете коротко обозначить затруднения которые возникли по мере выполнения - я либо смогу вам подсказать сразу (пока ваши воспоминания свежи) либо как минимум смогу подготовиться к следующему уроку и проговорить проблемные места.
Комментарии и подсказки к некоторым заданиям 1-10
Задание 2 (про логическую функцию)
Обычно работает заметить что функция всегда равна нулю (или всегда равна единице) и значения всех ее членов так же всегда одни и те же.
Из этого можно понять про какую-то переменную какому столбику она соответствует. Например w соответствует второму столбику.
А про какие-то переменные - по каким столбикам они могут быть распределены. Например может быть так что x и y - либо первый и третий столбики, либо первый и четвертый (но никак не третий и четвертый, из-за значения члена функции опирающегося на x и y).
Если больше закономерностей не видно, то делайте перебор - по столбикам возможны следующие четыре распределения: xwyz, ywxz (это были случаи про первый и третий столбики), xwzy, ywzx (первый и четвертый).
Выписав все эти четыре гипотезы - проверьте каждую: подставьте это распределение в таблицу и заполните ее полностью (или обнаружьте где-то несогласованность и т.о. переходите к следующей гипотезе).
В результате все кроме одной гипотезы отбросятся, а для единственной оставшейся гипотезы таблица должна достроится - не забудьте проверить что результат функции по этой таблице сходится.
Советы:
-
Если вы в тупике - не бойтесь перебора, но делайте это в конце если останется время (чтобы успеть другие более простые задания)
-
Не забывайте перечитывать условие - это может спасти вас от забывания правила про уникальность каждой строчки в таблице, приучите себя перечитывать условие в любой непонятной ситуации, в случае если задание кажется странным, и перед тем как окончательно записывать ответ
-
Не останавливайтесь как только нашли ответ - достройте для него матрицу истинности полностью, дважды проверьте что она подходит под условие (что результат функции сходится во всех строках и про уникальность строк)
-
Тратьте ваш бюджет времени разумно - если это задание вызывало затруднения на этапе тренировки - на ЕГЭ делайте его последним - лишь когда остальные задания будут выполнены (и желательно перепроверены)
Задание 5 (про кодирование и правило Фано)
Строите для всех букв (кодировка которых вам дана в условии) дерево кодирования (нолик - ответвление влево, единица - ответвление вправо, внизу на листьях дерева/тупиках - напишите закодированные буквы).
Прочитайте еще раз правило Фано. Поймите его. Поймите почему это то же самое что и в дереве кодирования нет ни одной буквы в середине дерева, иначе говоря они все в листьях, т.е. внизу - в тупиках.
Набросок решения этой задачи из Варианта 7 (сначала попробуйте решить сами, потом посмотрите на эту подсказку и извините пожалуйста за шакалов):
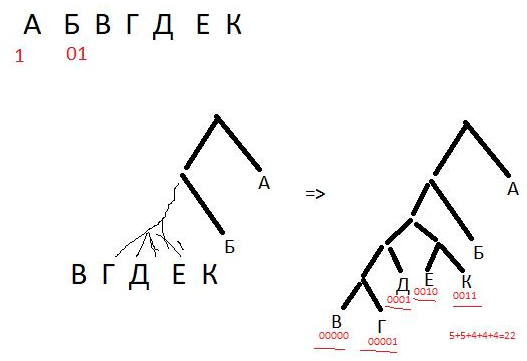
Задание 9 (про картинки и аудиозаписи)
В картинках все просто - есть двумерный массив пикселей, в каждом пикселе какой-то цвет.
Конкретный цвет кодируется конкретным числом, поэтому можете считать что в пикселях просто числа. Сколько цветов - столько вариантов значений этого числа.
Например 65536 цветов - это числа от 0 до 65535 (включительно) и чтобы закодировать цвет одного пикселя нужно 16 бит что то же самое что и 2 байта (т.к. \(65536=1024 \cdot 64=2^{10} \cdot 2^{6}\), один бит - это 0 или 1, один байт - это 8 битов, и легко запомнить что \(2^{10}=1024\) и значит \(2^{5}=32=\sqrt{1024}\)).
В аудиозаписях:
-
Если стерео (двухканальная) - то это просто две звуковые дорожки (для левого уха и для правого), т.е. по сути две аудиозаписи - просто домножаем на два
-
Частота дискретизации (в Гц - герцах) - сколько замеров звука в секунду, например если 1 кГц (т.е. килогерц - тысяча герц), то для каждой секунды звук сохранили в тысяче отдельных промежуточных моментов, т.е. тысяча замеров на секунду
-
Уровень квантования (например 65536) - как и с цветами, просто число вариантов записанного звука в каждый отдельный миг, а значит нам нужно найти степень двойки дающую данное число вариантов звука, и т.о. мы получим число бит нужное на один момент временина один аудиоканал
-
32-битное разрешение - то же что и уровень квантования, но с другой точки зрения - во сколько бит кодируется звук каждого отдельного мига, соответственно в данном случае соответствует \(2^{32}=4294967296\)-уровню квантования
Порешайте примеры (спросите у меня если что-то не сходится или остались вопросы/неуверенность) - 1, 2, 3.
Советы:
-
Когда посчитали ответ - перечитайте условие ВНИМАТЕЛЬНО (например то что аудиозапись стерео легко упустить беглым взглядом, т.к. это записано словом а не числом)
-
Перепроверьте что от вас требуют в ответе, минуты ли, секунды ли, округлить к ближайшему ли, или к большему ли (например в таком случае - какое минимальное количество)
-
Мбит и Мбайт - разные вещи, но легко вспомнить что из них что - первое это \(2^{32}\) бит, а второе - \(2^{32}\) байт. И то и то миллион, а миллион каких объектов - явно указано в названии
Задание 10 (комбинаторика)
Научитесь вспоминать комбинаторные формулы (например C из n по k) не зазубривая, а по логике, и не ленитесь проверять что они работают и что вы их вспомнили без ошибок - возьмите простой пример (например сколько способов выбрать два места из пяти), переберите все случаи руками, и сверьте что их выходит столько же сколько и по формуле.