Урок 15: построение прямой через точки - RANSAC
Итак, что делать если у нас есть сколько-то корректных (inliers, хоть они и могут быть шумными) точек с прямой, и сколько-то выбросов (outliers) - точек которые не имеют никакого отношения к прямой?
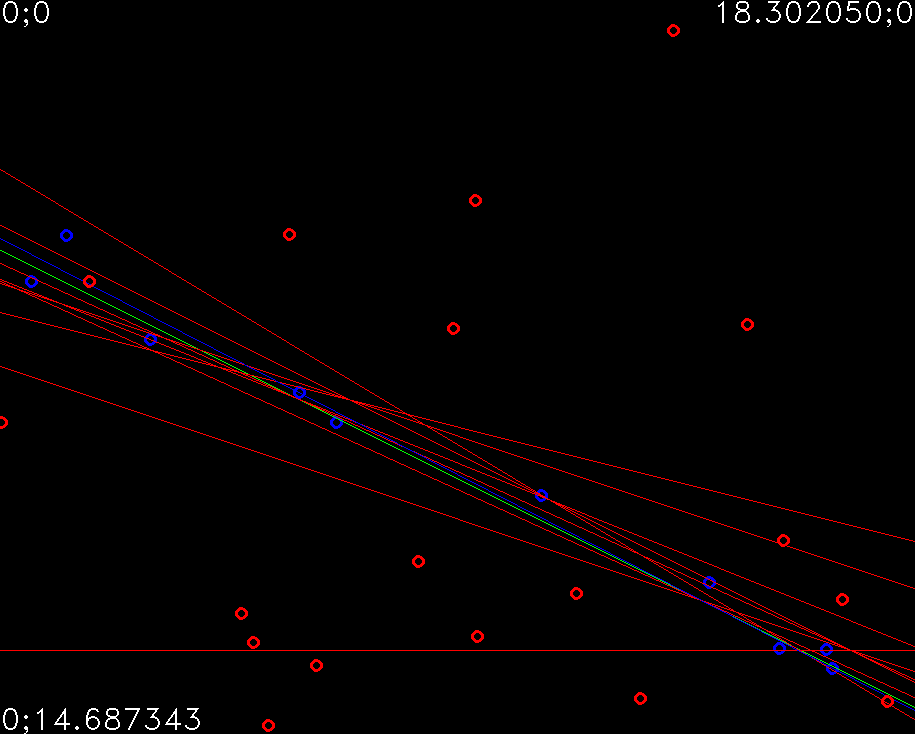
Для такой задачи есть очень широко применяемый подход - RANSAC (RANdom SAmple Consensus = консенсус через случайные гипотезы).
Идея такая - пусть мы хотим найти некоторый ответ (в данном случае прямую) по некоторому набору данных которые должны этому ответу подходить (в данном случае точки должены лежать на прямой-ответе).
Какой критерий качества нашего ответа? Т.е. насколько нам кажется прямая “правильной” для данного множества точек? Можно было бы считать среднее расстояние, но оно будет слишком сильно колебаться от выбросов - точек не имеющих отношения к прямой.
Давайте считать число точек которые находятся от прямой на каком-то разумном расстоянии, например не дальше чем на расстоянии 10 пикселей. Такая метрика устойчива к выбросам - они просто не будут засчитаны! Т.е. иначе говоря мы ищем прямую которая (с некоторой допустимой погрешностью) проходит через наибольшее число точек.
Тогда можно использовать следующий RANSAC алгоритм который по множеству точек найдет наиболее подходящую прямую:
1) Берем две случайные точки из нашего множества
2) Строим по этим точкам прямую A
3) Считаем число поддерживающих эту прямую точек (т.е. по сути число голосов за эту прямую, иначе говоря - число корректных замеров - т.е. количество inliers)
4) Повторяем шаги 1-3 например тысячу раз, а как ответ выдаем прямую с наибольшим числом голосов (т.е. с наибольшим числом inliers)
Интуиция в том что если даже корректных (inliers) точек с прямой всего лишь 10% (т.е. выбросов, outliers - 90%), то шансов угадать пару inliers-точек которые задают истинную прямую = 10% * 10% = 1%, а значит тысячи случайных угадываний должно быть достаточно.
Упражнения:
1) А что изменится если мы ищем параболу? (и у нас есть много точек лежащих около какой-то одной параболы + много выбросов)
2) А что изменится если точки будут в 3D и мы хотим найти плоскость на которой они лежат? Например это LIDAR-скан окружающего мира с беспилотного автомобиля и мы хотим найти плоскость земли:

3) А что как решить задачу поиска двух парабол? (если нам известно что 40% точек лежит на одной параболе, 40% точек лежит на другой параболе и 20% точек - выбросы)