1) Почему два экстремума?

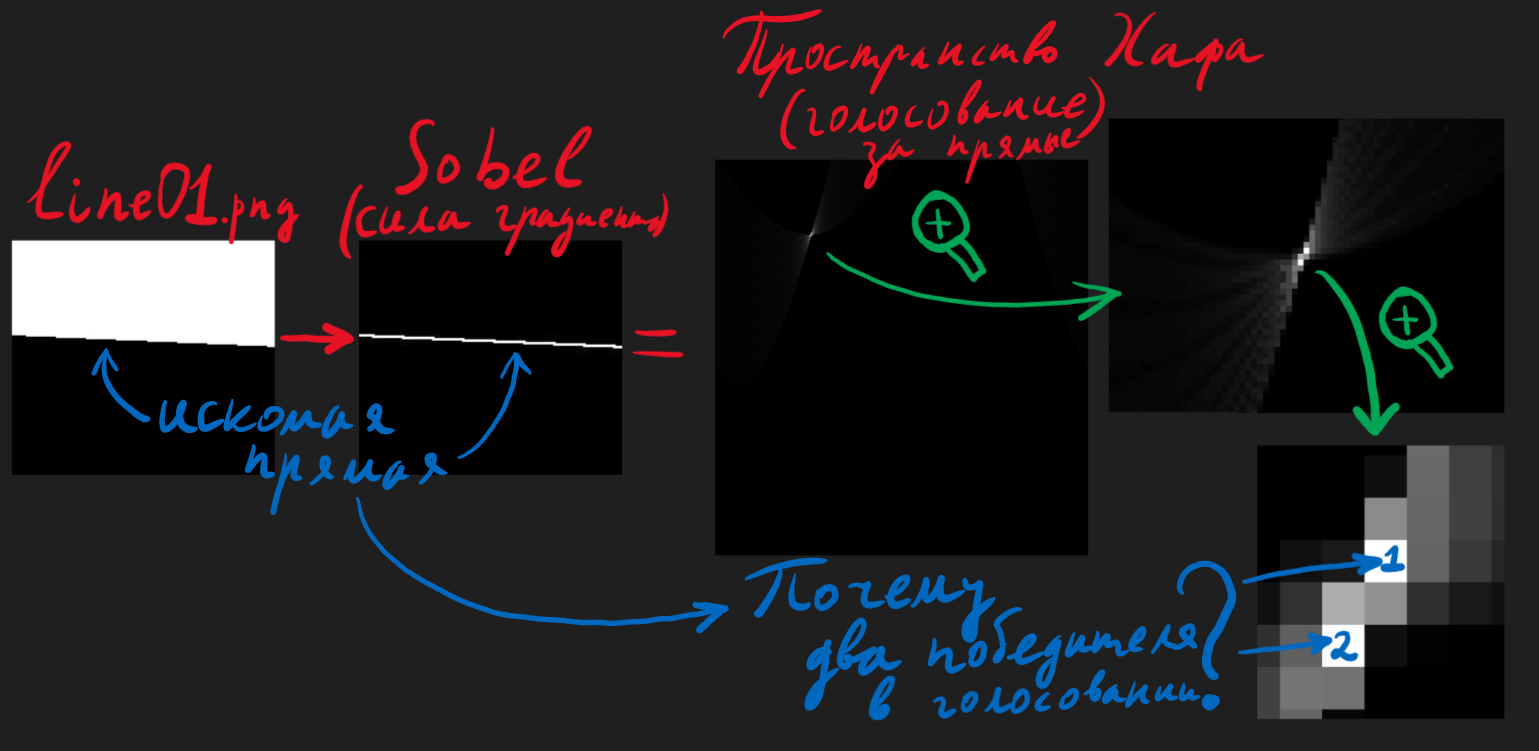
Итак пусть мы построили пространство Хафа, давайте пристально на него посмотрим на примере line01.png, почему хотя очевидно что прямая на картинке - одна - в пространстве Хафа у нас два победителя в голосовании? См. иллюстрацию:

Подсказка 1: вспомните как мы для каждой точки \(x_0, y_0\) добавляем голоса пучку прямых - мы пробегаем по всем \(\theta_0\), вычисляем для каждой из них соответствующее \(r_0=f(x_0, y_0, \theta_0)\) и добавляем голос в соответствующую корзину \(\theta_0, r_0\).

Подсказка 2: представьте что мы решаем традиционную задачу: отобразить график функции \(f(x)\), наивная реализация - пробежать по всему диапазону оси абсцисс и для каждого \(x_0\) рассчитаем \(y_0=f(x_0)\). Затем добавим на нашей картинке графика яркую точку в пиксель \(x_0, y_0\). Как будет выглядеть график например для функции \(f(x)=10 \cdot x\)?

После того как это исправите - наибольшие значения будут во-первых рядом, во-вторых один из них будет чуть больше других. Значит он и является нашей прямой-победительницей в голосовании:

2) Как автоматически искать прямую-победителя?

Прямая победила если является яркой точкой, иначе говоря если любая другая корзина голосования неподалеку набрала меньшее число голосов.

Определение Локальный экстремум (в картинке где каждый пиксель - сумма голосов за эту корзину) - это значение которое является максимальным в его окрестности 3х3. Иначе говоря все его соседи (по стороне и по диагонали - должны были оказаться меньше чем этот локальный экстремум). Если хотя бы один сосед набрал столько же или больше голосов чем мы - то мы не являемся локальным экстремумом.

Задание 1 Выведите для каждой картинке список параметров \(\theta_i, r_i\) для всех прямых (т.е. для всех пикселей в пространстве Хафа) которые после завершения голосования оказались локальными экстремумами. Сколько их для каких картинок оказалось?

3) Определите сколько голосов достаточно

Найдите самую популярную по числу голосов прямую. Пусть нас интересуют только те прямые - что хуже не более чем в два раза по числу голосов.

Задание 2 Сколько их оказалось для картинки line02.png и line12.png? А сколько должно было? Посмотрите в пространство Хафа, найдите эти экстремумы. Почему так вышло? Баг ли это? Если да - то как его поправить?

4) Если все еще обнаружается много разных прямых

Попробуйте добавить сглаживание пространства Хафа гауссовым блюром:

cv::Mat blurredHough;
int blurX = 5; // ширина сглаживания - по оси X
int blurY = 5; // высота сглаживания - по оси Y
cv::blur(hough, blurredHough, cv::Size(blurX, blurY)); // сглаживаем пространство Хафа (сглаженный результат в blurredHough)
hough = blurredHough; // заменяем сырое пространство Хафа на сглаженное
// и сохраянем его визуализацию на диск:
cv::imwrite("lesson08/resultsData/" + name + "_3_hough_blurred.png", hough*255.0f/max_accumulated);

Но посмотрите на пространство Хафа - оно для больших картинок гораздо более вытянутое в высоту, чем в ширину, поэтому давайте по вертикали сглаживать сильнее в соответствующей пропорции:

int blurX = 5;
int blurY = blurX * hough.rows / hough.cols;

Есть два нюанса:

1) Ширина и высота сглаживания всегда должна быть нечетной

2) Может быть так что пространство Хафа в высоту низкое (для маленьких картинок)

Поэтому поправляем эти два случая:

int blurY = blurX * hough.rows / hough.cols;
if (blurY % 2 == 0) {
    blurY = blurY + 1;
}
if (blurY < blurX) {
    blurY = blurX;
}

5) Если все еще обнаружается много разных прямых 2

Давайте заметим что большинство этих прямых - как будто очень похожи друг на друга. Давайте будем объединять две прямые в усредненную прямую в случае если угол отличается не больше чем, скажем, на 5 градусов и отступ от начала координат отличается не больше чем, например, на 10% ширины картинки.