Урок 8: поиск прямых 1 (преобразование Хафа)
Пусть есть картинка, и на ней мы уже знаем какие именно пиксели принадлежат границам объекта, или например мы знаем какие пиксели принадлежат горизонту на ландшафтной фотографии.
И пусть теперь мы хотим на базе этих пикселей определить какая прямая проходит через все этих пиксели максимально аккуратно.
Для начала вспомним какой вид имеет прямая (чтобы понять как ее параметризоваться - т.е. какими параметрами ее исчерпывающе описывать):
\(y = k \cdot x + b\) - стандартная формула в декартовых координатах, но у нее есть недостаток - она не умеет описывать вертикальные прямые (\(k\) начинает устремляться к бесконечности), а значит такая формула недостаточно обща и нам не подходит.
Давайте воспользуемся другой формулой в полярных координатах - любая прямая однозначно задается кратчайшим отрезком от начала системы координат до прямой:
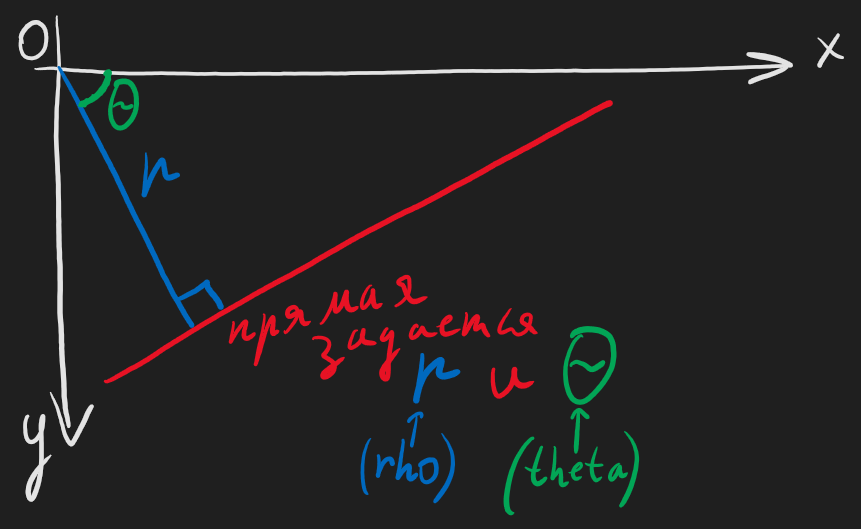
А раз прямая задается этим отрезком, то достаточно научиться исчерпывающе описывать этот отрезок - а он задается углом наклона и длиной - т.е. \(r\) (всегда положительное) и \(\theta\) (от \(0\) до \(2 \cdot \pi\)).
Тогда стандартная формула \(y = k \cdot x + b\) в декартовых координатах через эти параметры преобразуется в следующий вид:
\[y = - \frac{cos \theta}{sin \theta} \cdot x + \frac{r}{sin \theta}\]Эту формулу можно преобразовать:
\[r = x \cdot cos \theta + y \cdot sin \theta\]Теперь мы можем заметить, что если есть некая точка \(x_0\), \(y_0\) то все прямые содержащие эту точку имеют четкую зависимость между \(r\) и \(\theta\). Если бы мы однозначно знали что у нашей прямой второй параметр \(\theta=\theta_0\), то могли бы легко найти \(r=r_0\):
\[r_0 = x_0 \cdot cos \theta_0 + y_0 \cdot sin \theta_0\]Давайте посмотрим на пространство всех возможных кобинаций параметров \(r\), \(theta\) и прочертим в этом пространстве множество прямых содержащих такую точку \(x_0\), \(y_0\):
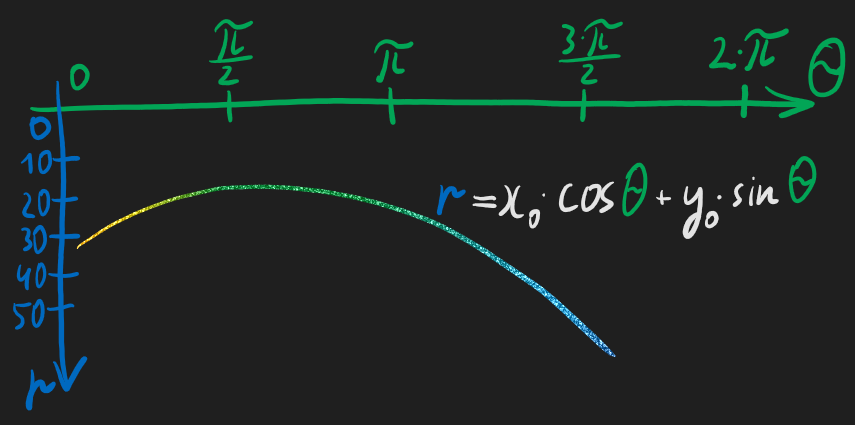
А что если у нас не одна точка \(x_0\), \(y_0\) а целых три точки лежащих на картинке на одной прямой? Давайте прочерчем для каждой из этих точек множество прямых которые через точку проходят:
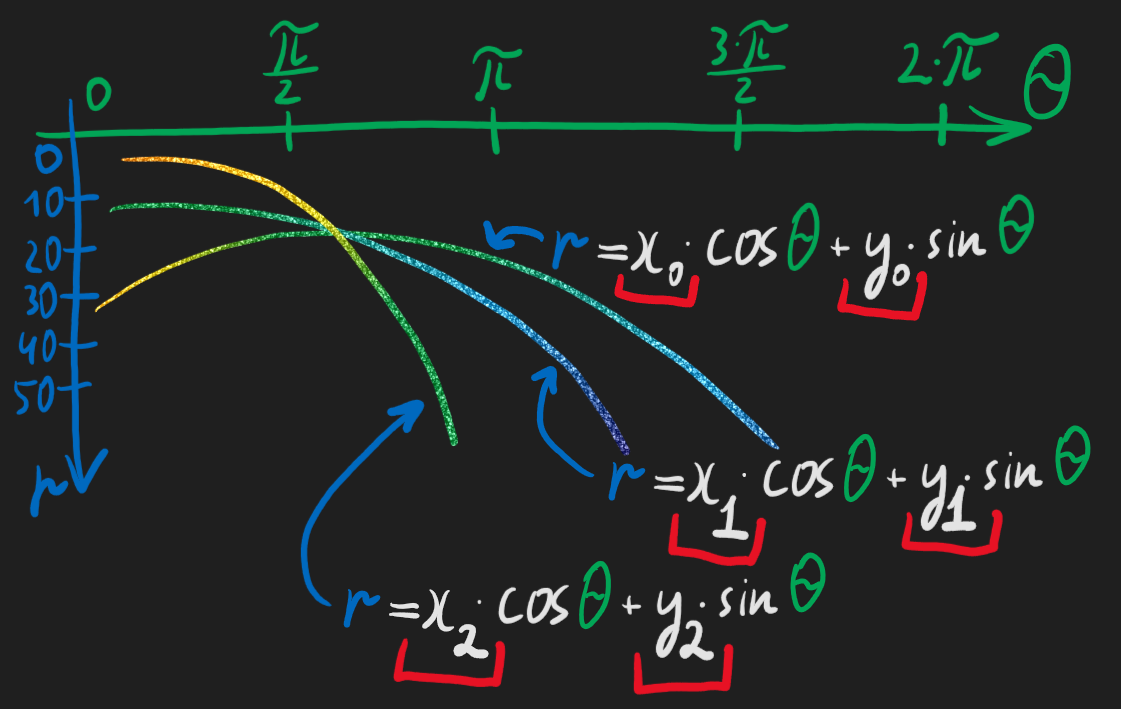
И оказывается что эти три кривулины, эти три множества прямых - пересекаются, и точка пересечения - это два параметра (\(r\) и \(theta\)) задающие прямую содержащую наши три точки:
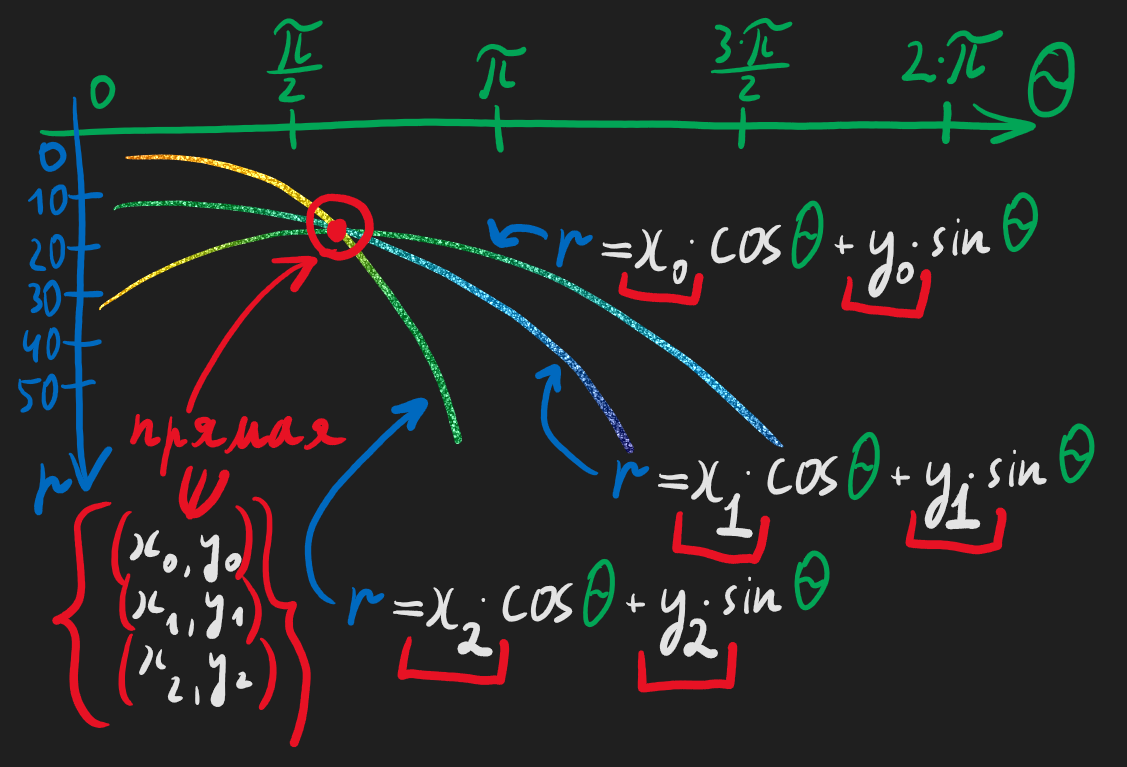
И из этого возникает идея - если есть точка которая голосует за искомую прямую, например искомый горизонт на фотографии - то эта точка проводит дополнительную кривулину подсказывая нам где находится истинная прямая.
Итого алгоритм:
1) Взяли картинку, оператором Собеля нашли точки-границы
2) Создали вещественную картинку размера \(max(\theta)\) на \(max(r)\) - т.е. 360 на \(\sqrt{width^2+height^2}\) - назовем ее аккумулятор, это пространство Хафа, в котором мы будем накапливать “голоса” за прямые
3) Для каждой точки-границы \(x_0, y_0\) с силой градиента \(strength\) (т.е. результатом оператора Собеля в этом пикселе):
3.1) Пробежим по всей оси \(\theta\) (т.о. от 0 до \(2 \cdot \pi = 360\) градусов) и высчитаем соответствующее \(r_0=x_0 \cdot cos \theta_0 + y_0 \cdot sin \theta_0\)
3.2) Для очередной пары \(\theta_0, r_0\) - добавим в картинку-аккумулятор голос нашего пикселя причем с весом: accumulator.at<float>(r0, theta0) += strength
4) Нарисуем картинку пространства Хафа и посмотрим сколько ярких точек - должно быть столько сколько прямых на картинке, например вот пара картинка и пространство Хафа:

