Геометрия: углы, предикат левого поворота, пересечения отрезков
Введение
Вектор можно представить ввиде двух чисел - смещение по оси \(x\) и смещение по оси \(y\). Поэтому разумно описать его ввиде следующего класса:
static class Vector {
final double x; // ключевое слово final указывает что эти поля
final double y; // не будут меняться в процессе существования объекта
public Vector(double x, double y) {
this.x = x;
this.y = y;
}
public double length() {
return Math.sqrt(x * x + y * y);
}
@Override
public String toString() {
return "Vector{" + x + ", " + y + '}';
}
}
Взгляните на пример вектора \(\vec{u}\):
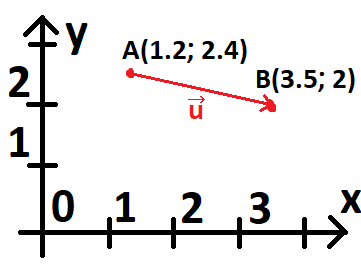
Упр Посчитайте какие в таком случае должны быть значения \(x\) и \(y\) у вектора \(\vec{u}\)?
Иначе говоря если бы мы захотели создать объект описывающий данный вектор в нашей программе мы бы написали:
Vector u = new Vector(2.3, -0.4);
Векторное произведение
Пусть есть два вектора:
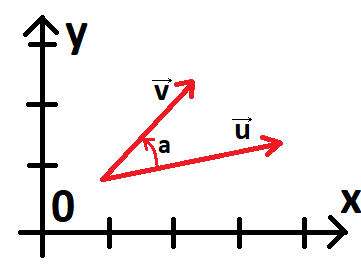
Опр Векторным произведением \(\vec{u} \times \vec{v}\) называется произведение длин векторов и знакового синуса ориентированного угла \(a\) от \(\vec{u}\) к \(\vec{v}\) (см. правило буравчика):
Все три множителя вполне понятны - просто произведение длин векторов (см. \(Vector.length()\) выше) и синуса угла между ними. Но обратите внимание что угол \(a\) знаковый.
Иначе говоря знак синуса зависит от того в каком направлении мы движемся от вектора \(\vec{u}\) (идущего первым в векторном произведении) к вектору \(\vec{v}\) (идущему вторым).
Если движение как на рисунке - т.е. против часовой стрелки, то угол положительный (\(a > 0\)).
Если движение по часовой стрелке, то угол отрицательный (\(a < 0\)). Например на данном рисунке это так для \(\vec{v} \times \vec{u}\).
Следствие Для любой пары векторов верно: \(\vec{u} \times \vec{v} = -(\vec{v} \times \vec{u})\).
Как же посчитать векторное произведение? Можно явным образом по определению, но есть формула проще:
Утв Векторное произведение можно посчитать следующим образом:
Давайте реализуем это ввиде функции:
static double crossProduct(Vector u, Vector v) {
return u.x * v.y - u.y * v.x;
}
Упражнение Проверьте что векторное произведение между парами этих векторов по данной формуле считается правильно (советую просто создать в программе объекты представляющие эти вектора и поперемножать их предложенной чуть выше функцией crossProduct):
-
Vector right = new Vector(1, 0);- просто единичный вектор вправо -
Vector up = new Vector(0, 1);- просто единичный вектор вверх -
Vector upRight45 = new Vector(Math.sqrt(2.0), Math.sqrt(2.0));- просто вектор вверх вправо под 45 градусов длины 2 -
Vector left = new Vector(-5, 0);- просто вектор влево длины 5 -
Vector down = new Vector(0, -3);- просто вектор вниз длины 3
Например удобно проверить как себя ведет векторное произведение исполнив этот код:
Vector right = new Vector(1, 0);
Vector up = new Vector(0, 1);
Vector upRight45 = new Vector(Math.sqrt(2.0), Math.sqrt(2.0));
Vector left = new Vector(-5, 0);
Vector down = new Vector(0, -3);
Vector[] vectors = new Vector[]{right, up, upRight45, left, down};
for (int i = 0; i < vectors.length; ++i) {
for (int j = 0; j < vectors.length; ++j) {
Vector u = vectors[i];
Vector v = vectors[j];
double result = crossProduct(u, v);
System.out.println(u + " x " + v + " = " + result);
}
}
Упражнение Убедитесь что в приведенном выше коде при исполнении:
-
Векторное произведение равно нулю при произведении вектора на самого себя, и что это согласуется с формулой
-
Векторное произведение от перемены порядка перемножаемых векторов просто меняет свой знак (т.е. что \(\vec{u} \times \vec{v} = -(\vec{v} \times \vec{u})\))
-
Посчитайте руками по явной формуле векторного произведение ожидаемый результат например перемножения
upRight45иleftи сверьте полученный результат с выведенным результатом программы
Утв Заметьте что теперь формулу синуса угла между векторами можно легко вывести:
Предикат левого поворта
Опр Пусть \(A, B, C\) - некотрые двухмерные точки, тогда
\(\operatorname{LeftTurn}(A, B, C) = \begin{array}{rl} 1 &, if \vec{AB}\times\vec{AC} > 0 \\ -1 &, if \vec{AB}\times\vec{AC} < 0 \\ 0 &, if \vec{AB}\times\vec{AC} ~= 0\end{array}\) - предикат левого поворота.
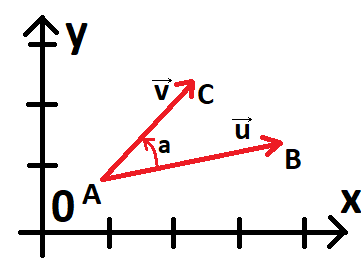
Иначе говоря если ввести \(\vec{u}=\vec{AB}\) и \(\vec{v}=\vec{AC}\), то предикат левого поворта:
-
Положителен если мы поворачиваем против часовой стрелки при движении от \(\vec{u}=\vec{AB}\) к \(\vec{v}=\vec{AC}\) (как на картинке)
-
Отрицателен если мы поворачиваем по часовой стрелки при движении от \(\vec{u}=\vec{AB}\) к \(\vec{v}=\vec{AC}\)
-
Равен нулю если вектора сонаправлены (обратите внимание что у нас неточные вычисления, поэтому равенство нулю должно быть с точностью до некоторого
double epsilon = 0.000001;)
Пересечение отрезков
Что такое \(\operatorname{LeftTurn}(A, B, C)\)? Заметим что предикат левого поворта:
-
Положителен если \(C\) слева от отрезка \(AB\)
-
Отрицателен если \(C\) справа от отрезка \(AB\)
-
Равен нулю если \(C\) лежит на отрезке \(AB\)
А что такое \(\operatorname{LeftTurn}(A, B, D)\)? То же самое, но на этот раз про точку \(D\) относительно отрезка \(AB\) (слева ли она от отрезка, справа ли, или лежит на отрезке).
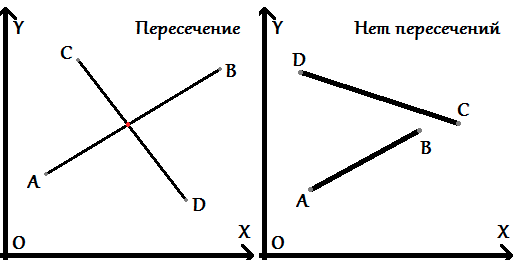
Утв 1 Отрезки \(AB\) и \(CD\) точно не пересекаются, если и \(C\) и \(D\) лежат по одну и ту же сторону от отрезка \(AB\).
Например если обе точки находятся слева от \(AB\), то и весь отрезок \(CD\) находится слева от \(AB\), а значит они не пересекаются!
Заметим что верно и симметричное утверждение:
Утв 2 Отрезки \(AB\) и \(CD\) точно не пересекаются, если и \(A\) и \(B\) лежат по одну и ту же сторону от отрезка \(CD\).
Давайте теперь научимся проверять отрезки на пересечение:
Утв 3 \(\operatorname{isIntersected}(AB, CD) = (\operatorname{LeftTurn}(A, B, C) != \operatorname{LeftTurn}(A, B, D))\) И \((\operatorname{LeftTurn}(C, D, A) != \operatorname{LeftTurn}(C, D, B))\)
Заметьте что это утверждение неверно в случае если отрезки лежат на одной прямой.
Упражнение Подумайте как разобрать этот особый случай.
Подсказка 1 Понять что этот случай имеет место можно проверив что предикаты левого поворота равны нулю.
Подсказка 2 Теперь зная что отрезки лежат на одной прямой достаточно проверить что \(A\) или \(B\) лежит между абсциссами и ординатами \(CD\). Либо наоборот - \(C\) или \(D\) лежит между абсциссами и ординатами \(AB\). Подробнее смотри - Пересечение отрезков.
Предупреждение
Если вы видите ошибку Exception in thread "main" java.util.InputMismatchException, то она у вас наблюдается т.к. вы используете русскую версию операционной системы, и поэтому
в связи с национальным стандартом вещественные числа разделяются через запятые (например \(1,5\)) а не через точки как в Америке (\(1.5\)).
Поэтому когда вы пытаетесь считать вещественное число \(1.5\) через scanner.nextDouble() он приходит в замещательство т.к. ожидает вещественные числа с дробной частью после запятой а не после точки.
Есть два варианта решения:
-
просто при локальном тестировании вводить числа через запятую, тогда локально все будет работать (на стороне mdl тоже будет работать т.к. там американский стандарт и тестовые данные ему соответствуют)
-
либо в коде явно указать сканеру, что он должен руководствоваться американским стандартом:
Scanner scanner = new Scanner(System.in);
scanner.useLocale(Locale.US);