Графы: хранение
Рекомендуемые источники
Основные определения теории графов
Введение
Пусть вам надо проложить маршрут из пункта А в пункт Б, как это сделать в программе? Для начала нужно придумать как вообще представить в вашей программе пространство в котором строится маршрут. В частности вам каким-то образом нужно описать что в целом в таких-то точках пространства возможно находится, из таких-то точек пространства можно перемещаться в такие-то за столько-то времени и т.п..
Графы
Один из самых простых и явных способов представить пространство - граф:
Определение Неориентированным графом называется пара \(G = (V, E)\), где \(V\) - множество вершин (т.е. точек в пространстве где может находиться двигающийся объект) и \(E\) - множество неориентированных ребер (т.е. двусторонние дороги соединяющие вершины и тем самым позволяющие между ними перемещаться за некоторое время в обе стороны).
Определение Ориентированным графом называется пара \(G = (V, E)\), где \(V\) - множество вершин и \(E\) - множество ориентированных ребер (т.е. односторонние дороги соединяющие вершины и тем самым позволяющие между ними перемещаться за некоторое время, при этом между некоторыми вершинами могут быть две встречные дороги - возможно даже разные по времени прохождения).
Представление матрицей смежности
Определение Матрицей смежности называется такая матрица, что для всех вершин \(u, v \in V: graph[u][v]=t\) - означает что есть ребро по которому можно пройти из \(u\) в \(v\) за время \(t\). Для удобства будем считать что \(t=-1\) или \(t=\infty\) означает отсутствие пути между данными вершинами. На самом деле ребра бывают с отрицательным временем, но мы такое рассматривать не будем.
Утв 1 В неориентированном графе матрица смежности симметрична, т.к. по определению неориентированного графа все ребра двусторонние, а значит \(graph[v][u] = graph[u][v]\).
Утв 2 Обычно время за которое можно дойти из пункта А в пункт А - ноль, поэтому в рамках нашего курса будем считать что \(graph[u][u]=0\), т.е. что диагональ матрицы смежности заполнена нулями.
Пример Пусть есть такой граф (на иллюстрации и часто в задачах вершины пронумерованы с единицы, но в рамках алгоритма обычно удобнее оперировать индексацией с нуля):
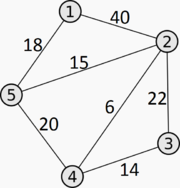
Матрица смежности \(graph[u][v]\) (отсутствие ребра обозначено как \(\infty\)):
\[\begin{bmatrix} 0 & 40 & \infty & \infty & 18\\ 40 & 0 & 22 & 6 & 15\\ \infty & 22 & 0 & 14 & \infty \\ \infty & 6 & 14 & 0 & 20\\ 18 & 15 & \infty & 20 & 0 \\ \end{bmatrix}\]Технические нюансы
В коде представить такую матрицу смежности лучше всего двумерным массивом, не забудьте инициализировать каждый внутренний массив явным образом:
// создаем массив массивов, здесь мы указали что всего массивов (т.е. строчек) будет N
// по одной строчке на каждую вершину u
int[][] graph = new int[N][];
for (int u = 0; u < N; ++u) {
// создаем строчку матрицы для каждой вершины u
// т.е. создаем N ячеек graph[u][vi] сразу для всех возможных vi
// (их всего N, поэтому создаваемый массив такого размера)
graph[u] = new int[N];
}
// ... не забудьте заполнить бесконечностями и нулями ...
for (int u = 0; u < N; ++u) {
for (int v = 0; v < N; ++v) {
graph[u][v] = scanner.nextInt(); // считываем длину ребра u<->v
}
}
Представление списком смежности
Заметим что если количество вершин \(V\), то занимаемая матрицей смежности память - \(O(V^2)\) независимо от того сколько ребер на самом деле есть в графе. Хотя если бы ребер было сильно меньше, скажем в среднем около 5 на вершину, то памяти для описания такого графа было бы достаточно порядка \(V*5\).
Более того, пусть мы хотим найти для какой-то конкретной вершины \(u\) ближайшую к ней вершину \(v\), сколько времени потребуется на это при использовании матрицы смежности? \(O(V)\) ведь нужно перебрать все возможные вершины \(v_i\), чтобы найти \(v=v_i\) с минимальным значением \(min(graph[u][v_i])\). Хотя если из вершины исходит всего пять ребер - достаточно было бы перебрать всего лишь их, чтобы найти среди них самый короткий.
Определение Повершинным списком смежности называется способ представить граф ввиде списка существующих ребер для каждой вершины.
Пример Пусть есть такой граф:

В таком случае повершинный список смежности выглядит так:
1: (40)->2, (18)->5
2: (40)->1, (15)->5, (6)->4, (22)->3
3: (22)->2, (14)->4
4: (14)->3, (6)->2, (20)->5
5: (18)->1, (15)->2, (20)->4
Т.е. для каждой вершины перечисляются ребра с их длинной и номером вершины в которую они ведут.
Технические нюансы
Как же представить в программе повершинный список смежности? Ведь в каждой вершине он может быть произвольной длины.
Достаточно для каждой вершины воспользоваться массивом произвольной длины, т.е. ArrayList-ом:
static class Edge {
public int to; // вершина в которую ведет данное ребро (может быть названо как v например)
public int weight; // вес, длина или время прохождения данного ребра (может быть названо как w, weight, t, time или l, length например)
public Edge(int to, int weight) {
this.to = to;
this.weight = weight;
}
}
public static void main {
// ...
// создаем список списков, в котором будет так что graph.get(u) - это список ребер исходящих из вершины u
ArrayList<ArrayList<Edge>> graph = new ArrayList<ArrayList<Edge>>();
for (int u = 0; u < N; ++u) {
// создаем пока что пустой список ребер исходящих из вершины u
graph.add(new ArrayList<Edge>());
}
for (int e = 0; e < E; ++e) {
int u = scanner.nextInt();
int v = scanner.nextInt();
int time = scanner.nextInt();
// данный пример для неориентированного графа, поэтому ребро идет в обе стороны:
graph.get(u).add(new Edge(v, time)); // u -> v
graph.get(v).add(new Edge(u, time)); // v -> u
}
}
Сортировка сложных объектов (например ребер)
На прошлом занятии мы научились сортировать массивы чисел по возрастанию встроенной функцией Arrays.sort(int[] xs).
Но что делать если мы хотим отсортировать например список ребер (т.е. список из class Edge) для какой-то вершины \(u\) (т.е. \(graph[u]\), т.е. мы хотим отсортировать элементы списка ArrayList<Edge>)
Достаточно ввести порядок над ребрами, т.е. решить что значит что одно ребро больше другого. Например в нашем случае мы считаем что то ребро больше, у которого больше номер вершины в которую он идет.
Java требует это сформулировать ввиде функции int compare(Edge a, Edge b) которая возвращает результат по следующим правилам:
-
Возвращает отрицательное число, если \(a < b\) (т.е. если \(a.to < b.to\))
-
Возвращает ноль, если \(a == b\) (т.е. если \(a.to == b.to\))
-
Возвращает положительное число, если \(a > b\) (т.е. если \(a.to > b.to\))
Итого чтобы отсортировать ребра исходящие из каждой вершины достаточно написать так:
ArrayList<ArrayList<Edge>> graph = new ArrayList<ArrayList<Edge>>();
// ...
for (int u = 0; u < n; ++u) {
// Сортируем список для вершины номер u, т.е. graph.get(u) возвращает список ребер ArrayList<Edge>
graph.get(u).sort(new Comparator<Edge>() {
@Override
public int compare(Edge a, Edge b) {
return a.to - b.to; // заметьте что таким образом мы очень легко реализовали требуемую функцию
// убедитесь что она соответствует трем правилам написанным выше
}
});
}
Альтернативный более лаконичный способ написать то же самое - воспользоваться так называемой лямбда-функцией:
ArrayList<Edge>[] graph = new ArrayList[N];
// ...
for (int u = 0; u < n; ++u) {
graph[u].sort((a, b) -> a.to - b.to); // здесь написана та же функция что и выше - просто по-другому
}
Обратите внимание на ошибку
Если вы видите ошибки вроде этой:
.java:9: error: unmappable character (0xD0) for encoding US-ASCII
public int to; // ?????????????? ?? ?????????????? ??????????
То у вас в коде есть комментарии на русском - вам нужно удалить их перед отправкой, т.к. они сводят mdl с ума.